วันอาทิตย์ที่ 22 มกราคม พ.ศ. 2555

คณิตตรรกศาสตร์

คณิตตรรกศาสตร์

ในสาขาคณิตตรรกศาสตร์มีการแยกสัจพจน์ออกเป็นสองรูปได้แก่ "สัจพจน์ที่เป็นตรรกะ" และ "สัจพจน์ที่ไม่เป็นตรรกะ" ซึ่งคล้ายคลึงกับการแยก "สัจพจน์" กับ "มูลบท" ในสมัยก่อนตามลำดับ

 สัจพจน์ที่เป็นตรรกะ

ในภาษารูปนัยมีสูตรเชิงตรรกะตายตัวที่ถือว่าสมเหตุสมผลโดยสากล (Universally Valid) สูตรนี้จะสอดคล้องกับค่าความจริงทุกค่า โดยปกติแล้วการกำหนดสัจพจน์ที่เป็นตรรกะจะกำหนดให้มีจำนวนน้อยที่สุดที่เพียงพอที่จะพิสูจน์สัจนิรันดร์ในภาษาทั้งหมดได้ ยกเว้นแต่ตรรกะภาคแสดง(predicate logic) จะมีการเพิ่มสัจพจน์มากกว่าที่จำเป็น เพื่อพิสูจน์ค่าความจริงของประโยคที่ไม่เป็นสัจนิรันดร์ภายใต้เงื่อนไขที่รัดกุม

 ตัวอย่าง

 ตรรกศาสตร์เชิงประพจน์
ในตรรกศาสตร์เชิงประพจน์ โดยปกติแล้วจะมีสูตรเชิงตรรกะที่กำหนดให้เป็นสัจพจน์ดังนี้ เมื่อให้ ϕ, χ, and ψ เป็นสูตรเชิงตรรกะใดๆ ในภาษารูปนัย ภายใต้ตัวดำเนินการทางตรรกศาสตร์เพียงสองอันได้แก่ "\neg" นิเสธของประพจน์ และ "\to\," เงื่อนไข (ตรรกศาสตร์) ที่เชื่อมประพจน์จากเหตุไปสู่ผล:
  1. \phi \to (\psi \to \phi)
  2. (\phi \to (\psi \to \chi)) \to ((\phi \to \psi) \to (\phi \to \chi))
  3. (\lnot \phi \to \lnot \psi) \to (\psi \to \phi).
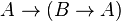แต่ละรูปแบบล้วนเป็น เค้าร่างสัจพจน์(Axiom Schema) ซึ่งสามารถผลิตสัจพจน์อื่นได้จำนวนไม่จำกัด ยกตัวอย่างเช่นให้ A, B C แทน ตัวแปรเชิงประพจน์ ใดๆ A \to (B \to A) และ (A \to \lnot B) \to (C \to (A \to \lnot B)) ก็ล้วนแต่เป็นผลมาจากเค้าร่างสัจพจน์ที่ 1 ดังนั้นจึงประโยคทั้งสองจึงเป็นสัจพจน์ไปด้วย
เค้าร่างสัจพจน์ทั้งสามเมื่อรวมกับ modus ponens นั้นเพียงพอที่จะพิสูจน์สัจนิรันดร์ในตรรกศาสตร์เชิงประพจน์ทั้งหมดได้ แต่การหยิบแค่สองเค้าร่างนั้นไม่เพียงพอที่จะพิสูจน์สัจนิรันดร์ทั้งหมด จำนวนของสัจพจน์ของตรรกเชิงประพจน์ดังกล่าวจึงน้อยที่สุดแล้วที่จะพิสูจน์สัจนิรันดร์ทั้งหมดได้ นอกจากนั้นแล้ว เรายังสามารถสร้างเค้าร่างสัจพจน์อื่นๆ ภายใต้ตัวดำเนินการทางตรรกศาสตร์ได้อย่างอิสระจากเค้าร่างสัจพจน์ดังกล่าว [1] และเค้าร่างสัจพจน์นี้ยังใช้ในตรรกศาสตร์ภาคแสดงแต่ต้องเพิ่มสัจพจน์ที่เป็นตรรกะอื่นๆ ลงไป เช่นสัจพจน์ของตัวบ่งปริมาณ เป็นต้น[2]
คณิตตรรกศาสตร์
สัจพจน์แห่งความเท่ากัน ให้ \mathfrak{L} เป็นภาษาอันดับหนึ่ง และ x เป็นตัวแปรใดๆ บนภาษานั้น จะได้ว่า
x = x\,
เป็นสูตรที่สมเหตุสมผล
นั่นหมายความว่าสำหรับตัวแปร x ใดๆ การเขียน x = x ย่อมเป็นสัจพจน์เสมอ
เค้าร่างสัจพจน์สำหรับตัวอย่างสากล ให้ \phi\, เป็นสูตรบน\mathfrak{L} ซึ่งเป็นภาษาอันดับหนึ่ง ตัวแปรx และเทอม t ซึ่งสามารถ แทนค่าได้บน x ใน ϕ จะได้ว่า
\forall x \, \phi \to \phi^x_t
เป็นสูตรที่สมเหตุสมผล
โดยที่สัญลักษณ์ \phi^x_t แทนสูตร φ เมื่อแทนสูตร t ลงไปใน x นั่นหมายความว่าเมื่อเราระบุว่า สำหรับทุกๆ x แล้วสูตร \phi^x_t เป็นจริง ดังนั้น เมื่อแทนสูตร t ลงไปใน ϕ ซึ่งเป็นกรณีเฉพาะกว่าก็ย่อมเป็นจริงด้วย
เค้าร่างสัจพจน์สำหรับการมีอยู่จริงโดยทั่วไป ให้ \phi\, เป็นสูตรบน\mathfrak{L} ซึ่งเป็นภาษาอันดับหนึ่ง ตัวแปรx และเทอม t ซึ่งสามารถ แทนค่าได้บน x ใน ϕ จะได้ว่า
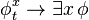
\phi^x_t \to \exists x \, \phi
เป็นสูตรที่สมเหตุสมผล
เขียนโดย ที่

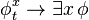
ไม่มีความคิดเห็น:

แสดงความคิดเห็น

สมัครสมาชิก: ส่งความคิดเห็น (Atom)